Uno de nuestros trabajos frecuentes en AKIS International y E-STRATOS consiste en analizar grandes matrices de datos. Cada día es más fácil medirlo (y registrarlo) todo, pero frecuentemente acaba resultando muy difícil extraer la información contenida en los números. Aunque existen muchos tipos de enfoques distintos, pocas herramientas son tan potentes como las incluidas en el universo del análisis multivariante.
Desde que comenzamos a trabajar con estas técnicas de la mano del profesor Ferran Gatius hace ya bastantes años, hemos integrado su aplicación a distintos campos como la descripción de procesos bioquímicos, la inactivación de enzimas o la caracterización de frutas, demostrando que pueden ser muy útiles para llegar rápidamente a las mismas conclusiones que con análisis cinéticos mucho más largos y que requieren el desarrollo de ecuaciones bastante complejas. También las hemos aplicado para conocer qué variedades de un cultivo funcionan mejor, para determinar las mejores condiciones de eficacia de tratamientos fertilizantes o fitosanitarios o para comprender las dinámicas poblacionales de algunas plagas.
Pero a pesar de la facilidad de su uso e interpretación (y aunque es cierto que el proceso requiere conocimientos técnicos y cierta experiencia), sigue existiendo un gran desconocimiento del enorme potencial del análisis multivariante para revelar los secretos escondidos en grandes cantidades de datos. En este post intentaré explicar de manera sencilla la razón fundamental por la que una de estas técnicas, el Análisis de Componentes Principales (Principal Component Analysis, PCA), es una herramienta tan potente. Ruego a los matemáticos y teóricos que me disculpen, pues esta página no está escrita con la finalidad de explicar cómo funcionan los algoritmos, sino de mostrar la utilidad del PCA al público no iniciado.
Hagamos un pequeño ejercicio. Imaginemos que tenemos los resultados de la observación de dos variables (que llamaremos x e y) sobre 10 muestras:
Muestra | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
x | 8,00 | 3,00 | 10,00 | 4,00 | 5,00 | 9,00 | 1,00 | 6,00 | 2,00 | 7,00 |
y | 7,50 | 3,50 | 10,50 | 3,50 | 5,25 | 9,50 | 0,50 | 5,75 | 2,25 | 7,50 |
A simple vista es difícil hacernos una idea de la relación entre ambas variables. Para extraer conclusiones podemos ayudarnos de una representación gráfica. Afortunadamente sólo tenemos 2 variables, así que para interpretar los datos podemos representarlos en un gráfico de 2 dimensiones:
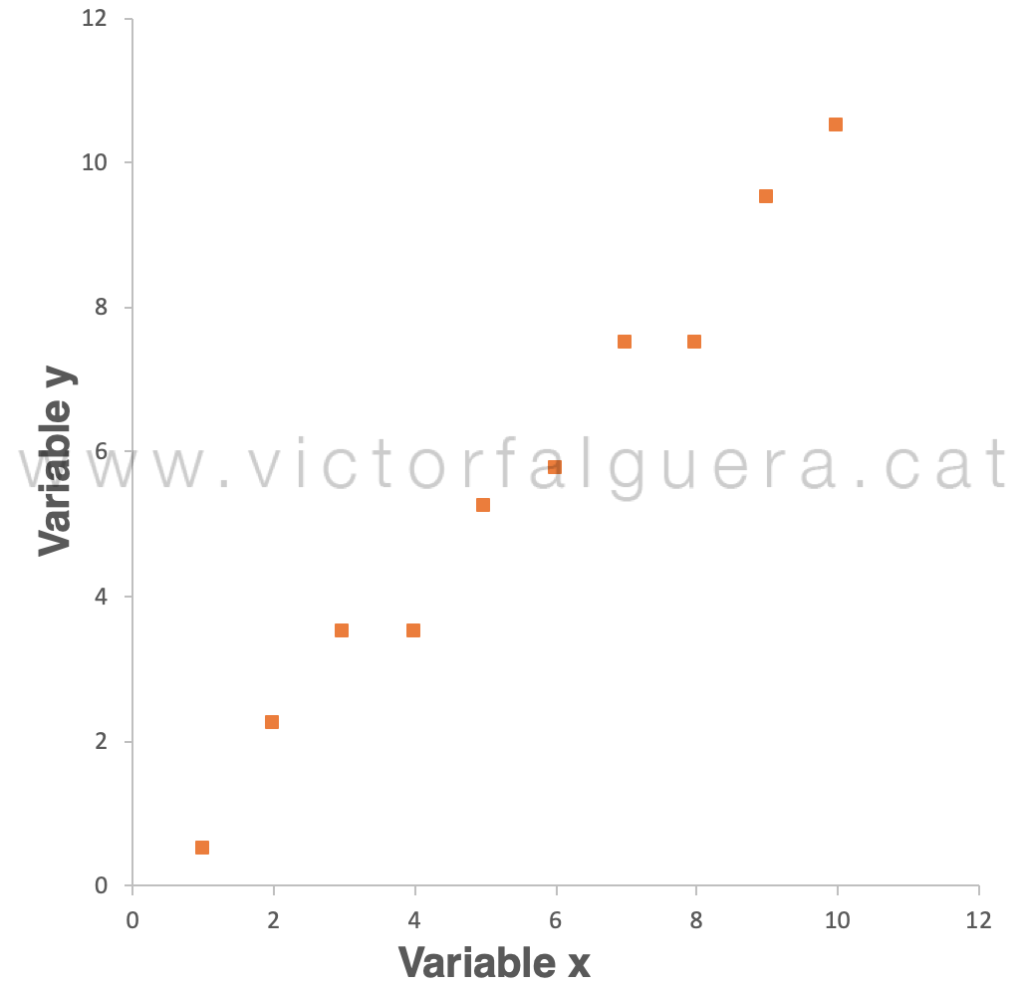
Aquí ya vemos que existe una “tendencia” y que, probablemente, podremos encontrar una forma de “explicar” esta relación entre nuestras variables x e y. Dicho de otra forma, parece evidente que los datos tienen una cierta “estructura”.
Imaginemos que, para nuestro entendimiento, es demasiado complicado explicar lo que está pasando utilizando las dos variables (x e y). ¿Qué pasaría si quisiéramos explicar esta estructura utilizando sólo una variable en vez de dos? En principio, deberíamos elegir si lo explicamos mediante la variable x o por el contrario utilizamos la variable y. Si elegimos describir nuestros datos sólo a partir de la variable x, el “error” que estaríamos cometiendo corresponde a la distancia de cada punto en el gráfico hasta el eje x:
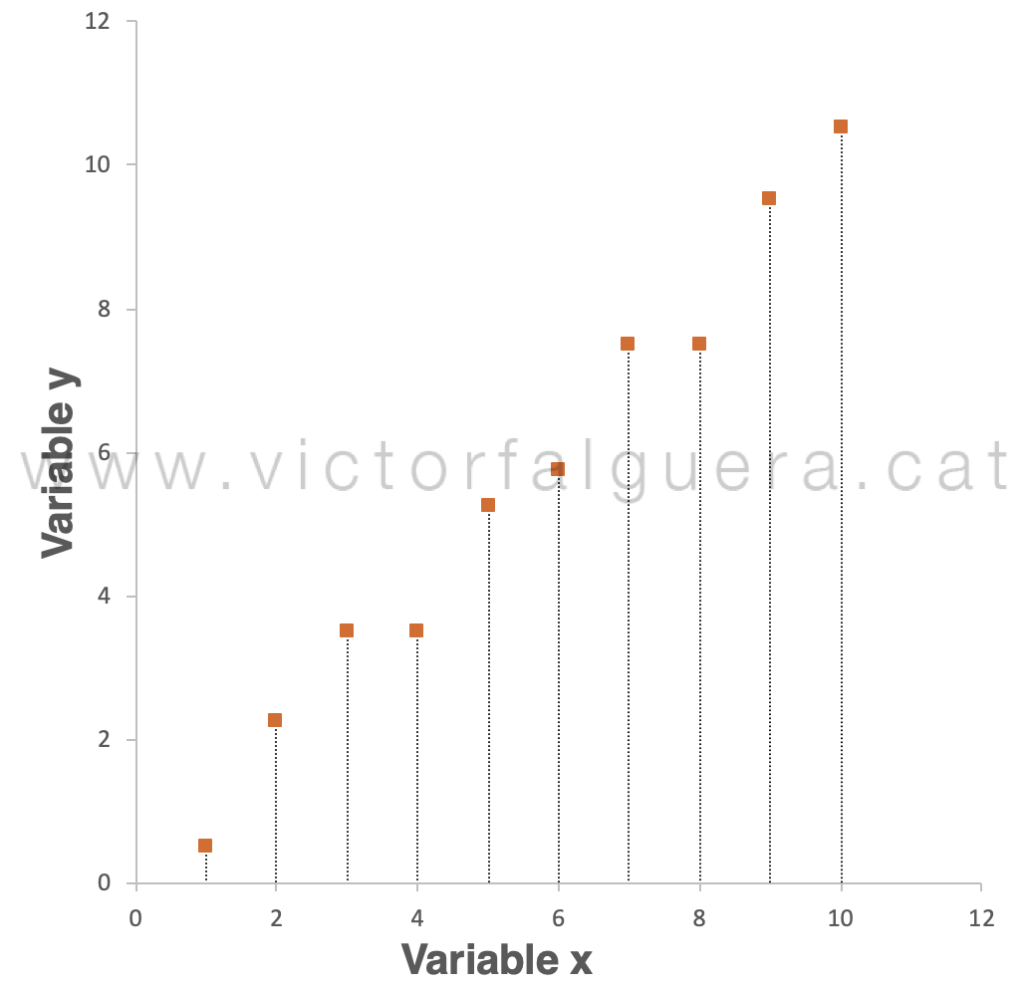
En términos matemáticos, podemos calcular este error (raíz del error cuadrático medio, RMSE) en 6,20 unidades. Si tenemos en cuenta que el rango de valores que estamos observando se mueve aproximadamente del 0 al 10, desde luego sería mejor opción tirar dos dados al aire que describir los datos utilizando solamente la variable x. Si por el contrario elegimos la variable y, el error corresponde igualmente a la distancia de los puntos a este eje:
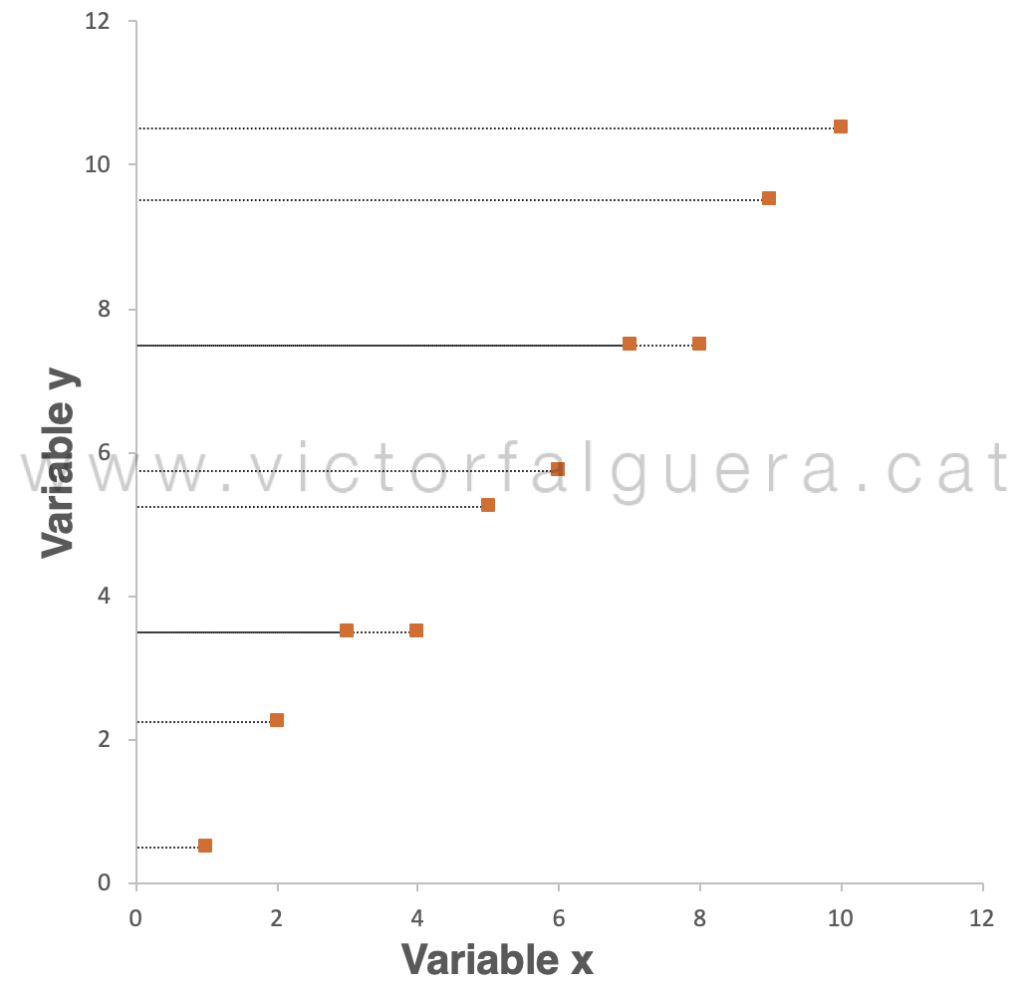
En este caso, el error medio es de 6,35 unidades. Tampoco parece la mejor opción. Sin embargo, lo que parece bastante evidente es que podemos encontrar la manera de dibujar una línea recta que se ajuste bastante bien a los datos, es decir, que quede cerca de todos los puntos (en este caso, algo parecido a la regresión lineal de toda la vida):
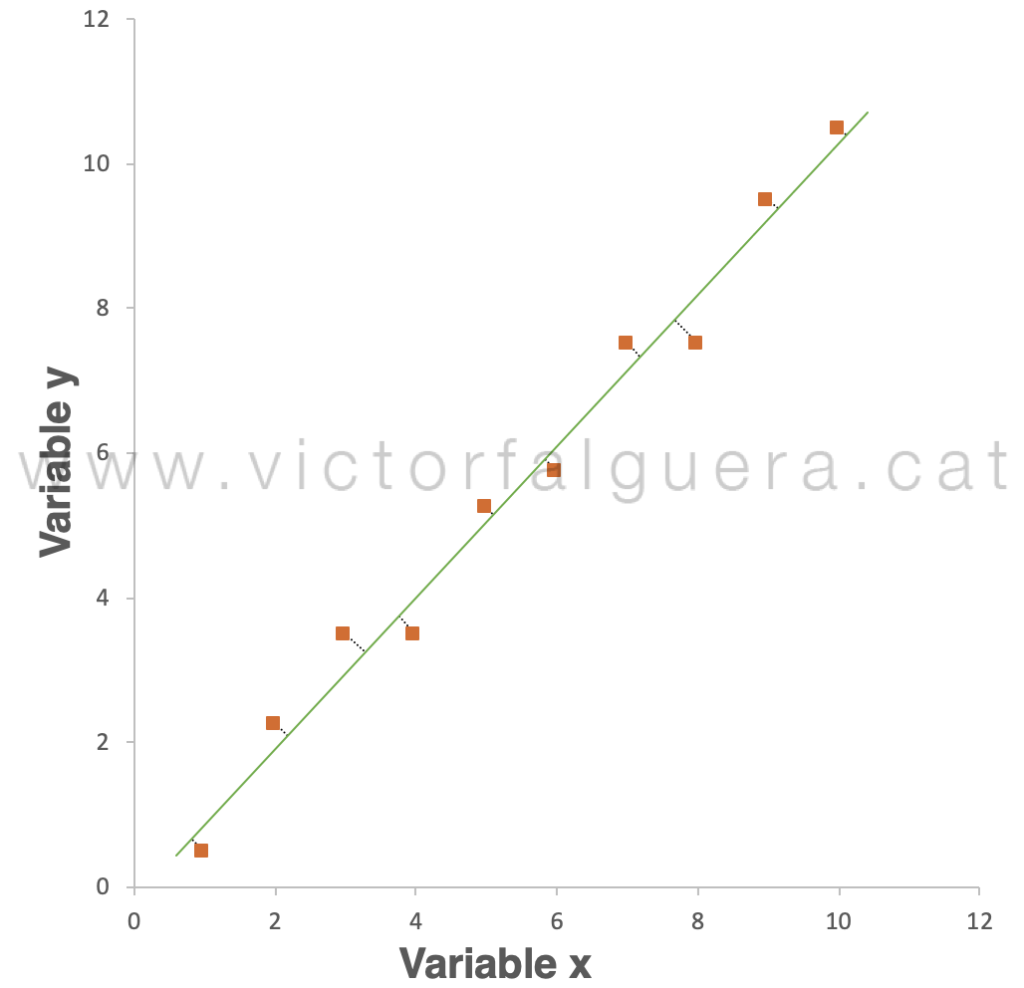
Ahora, si pudiéramos describir los datos sólo utilizando esta línea verde, solamente estaríamos cometiendo pequeños errores (las distancias representadas por las líneas de puntos). En otras palabras, lo que realmente estaríamos explicando es la proyección de los datos sobre este eje:
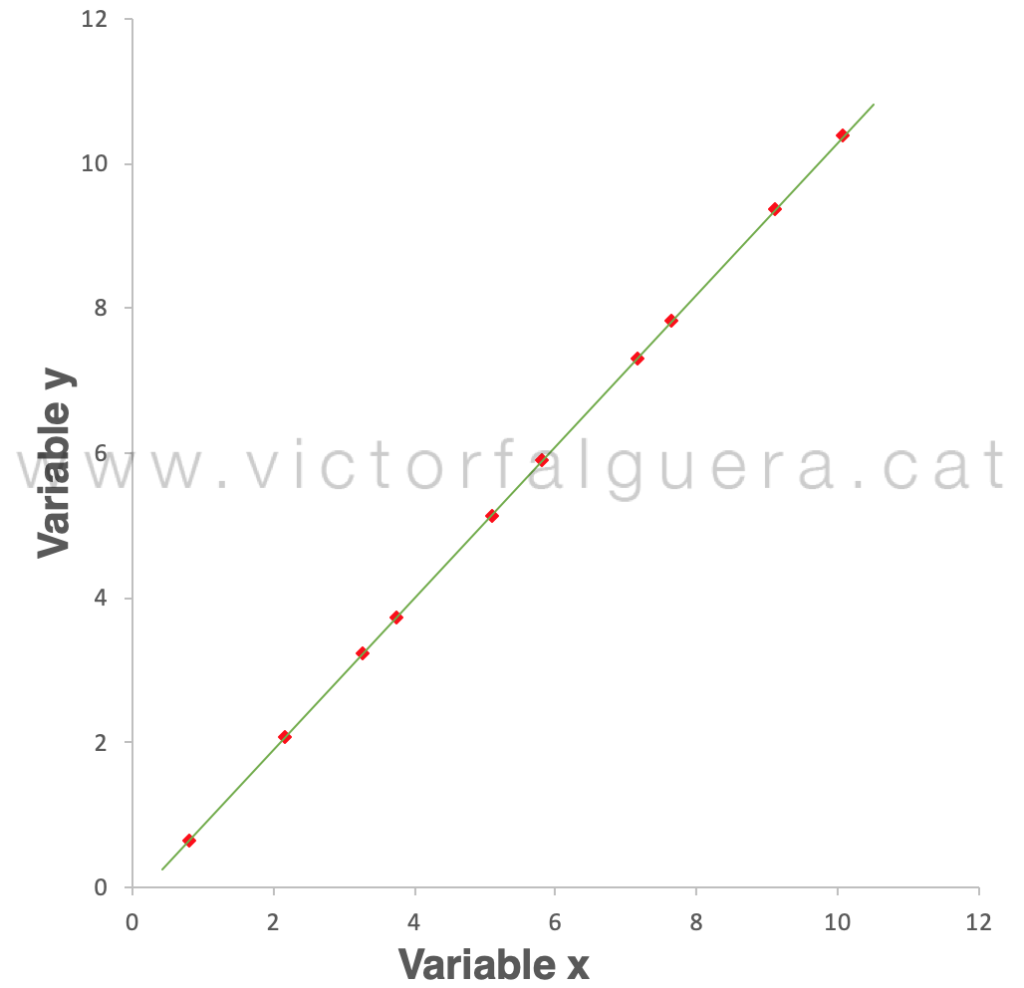
La diferencia entre los dos últimos gráficos, es decir, el error que estaríamos cometiendo, es de sólo 0,28 unidades. Esto está mejor, ¿no? Solamente nos quedaría decidir si “nos compensa” asumir este error a cambio de la simplicidad de poder explicar los datos con una sola variable en lugar de dos.
Pero nos queda la parte más importante, que es la de definir esta nueva variable. Las dos variables iniciales tenían un significado físico (o químico, o espiritual), pero la nueva variable (que llamaremos r) a priori es sólo un instrumento matemático que nos sirve para simplificar la explicación (realmente, la interpretación del significado de esta nueva dimensión forma parte del trabajo posterior al análisis). Por tanto, ¿cómo la definimos?
Sin entrar en procedimientos de cálculo, vamos a intentar recordar cómo hemos “decidido” este nuevo eje. El problema más importante que teníamos al intentar describir los datos utilizando solamente la variable x, es que existía mucha distancia entre los datos y el eje x, lo que significaba que estábamos cometiendo un error muy grande. Y eso se explica porque la dirección en la que vemos claramente que evolucionan los datos no estaba alineada con este eje x (ambas direcciones forman un ángulo de aproximadamente 45º).
Hemos dibujado el nuevo eje (verde, r) de forma que quedara lo más cerca posible de todos nuestros puntos, y lo hemos conseguido alineándolo con la dirección en la que los puntos se reparten, o en otras palabras, en la dirección en la que varían más los datos. Pues bien, esa dirección de máxima varianza es lo que se conoce como el primer Componente Principal (PC1).
Si queremos hilar más fino y no estamos dispuestos a asumir ese error de 0,28 unidades, ¿cómo dibujaríamos un nuevo eje de coordenadas, complementario al r, que nos permitiera explicar también esa pequeña cantidad de información? Evidentemente este nuevo eje, al que podemos llamar s, debería ser perpendicular (ortogonal), porque de lo contrario parte de la información se podría proyectar sobre el otro eje r (y tendríamos información redundante, que es precisamente lo que no queremos):
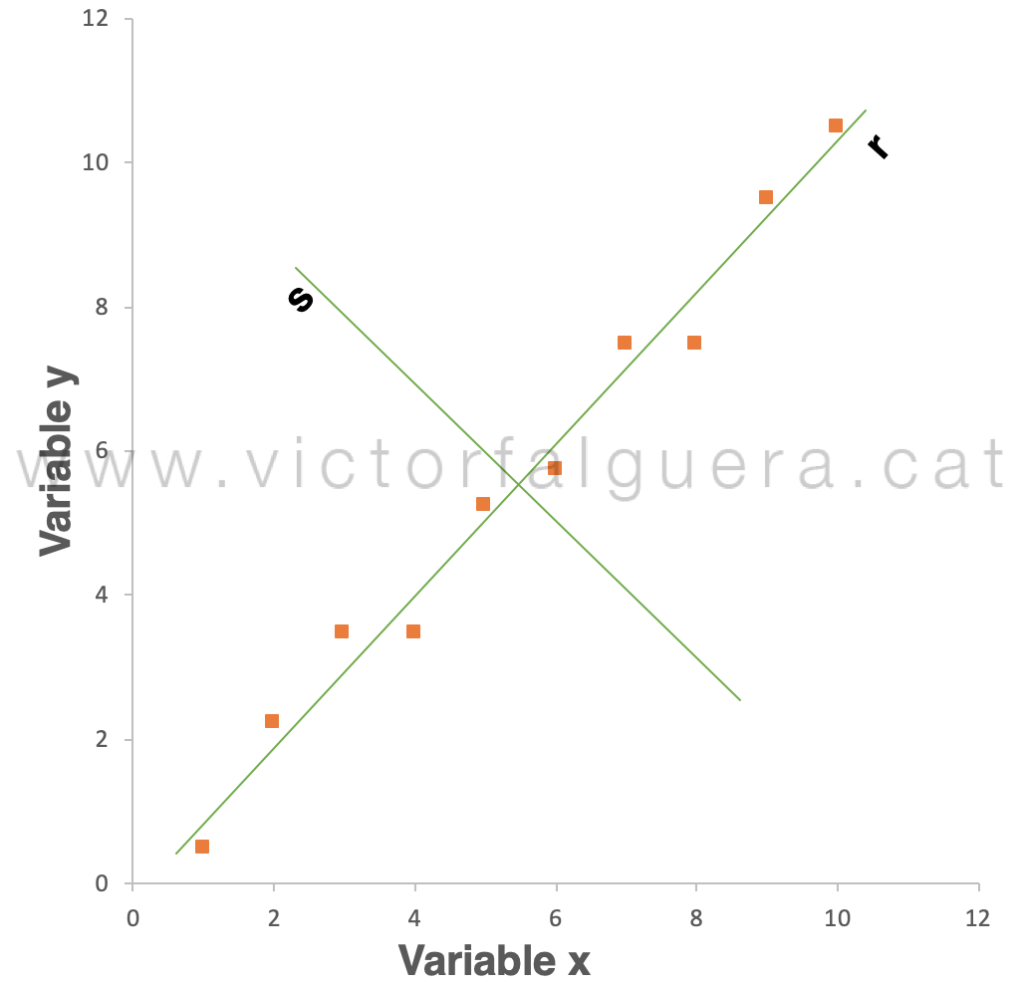
Ahora, la información que no explicaba la variable r sí se puede explicar con la variable s. Es decir, podemos definir la variable s como la segunda dirección de máxima varianza, o lo que es lo mismo, como el segundo Componente Principal (PC2). Los datos siguen siendo los mismos, pero hemos cambiado la forma de explicarlos (el punto de vista, o el sistema de coordenadas), con la diferencia de que con una sola de las variables (r, el primer Componente Principal) estamos explicando la inmensa mayoría de su estructura. Si rotamos la vista y dibujamos los puntos en el nuevo espacio:
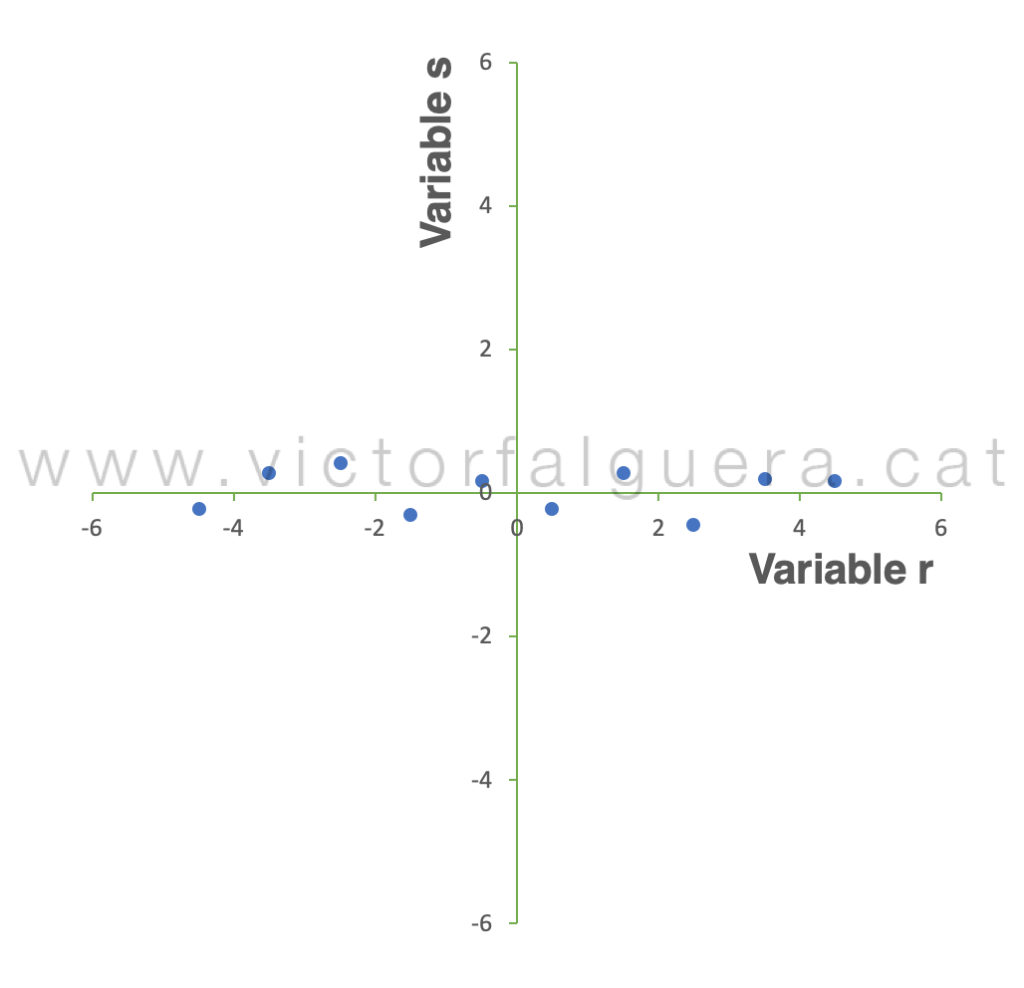
Si queremos explicar los datos utilizando solamente la variable r en este nuevo espacio, debemos nuevamente proyectar los puntos sobre este eje:
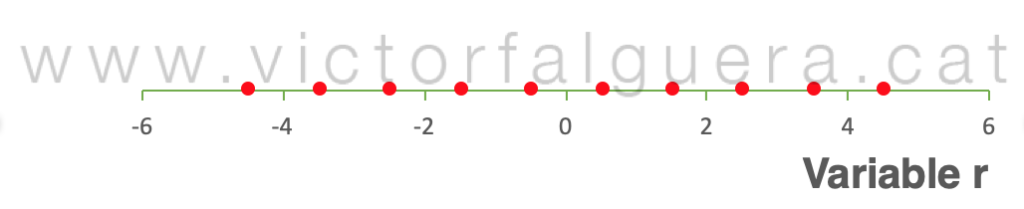
Así conseguimos explicar los datos con solamente una variable y asumiendo un error muy pequeño. Este procedimiento que sirve para reducir el número de variables utilizadas en la descripción de un conjunto de datos se llama reducción dimensional, y es la base de muchas de las ventajas del Análisis de Componentes Principales.
***
En nuestro ejemplo, toda la información contenida en el espacio original que definían los ejes x e y se puede explicar también en el nuevo espacio que definen los ejes r y s. Si quisiéramos dibujar un tercer eje para obtener un gráfico en 3 dimensiones, el valor de la nueva variable sería la misma para todos los puntos: 0. Es decir, podríamos colocar los datos en un gráfico en 3 dimensiones, pero los veríamos todos en el mismo plano. Por tanto, el máximo número de Componentes Principales (PC) que podemos encontrar es igual al número de variables originales. Sin embargo, en el sistema de coordenadas descrito por los PC cada uno explica una parte de la estructura más pequeña que el anterior, lo que de cara a la interpretación de los datos facilita muchísimo las cosas.
Si solamente tenemos 2 variables originales el método tampoco nos aporta mucho, pero si imaginamos una matriz con cientos (o miles) de muestras y cientos (o miles) de variables, la cosa cambia, ¿verdad? ¿Cómo dibujamos un gráfico que tenga miles de dimensiones para poder interpretar los datos? La buena noticia es que, aunque tengamos miles de variables originales, si la matriz es suficientemente robusta la mayoría de la varianza original puede explicarse observando el espacio que definen los primeros PC (y, además, vamos a saber el % de la varianza global que explica cada uno).
Además, si una variable está muy correlacionada con otra (aporta una información similar), con una de ellas nos basta. Como cada nuevo PC aporta sólo la explicación de la información no contenida en los anteriores, la que es redundante se elimina. ¿Y si además pudiéramos analizar conjuntamente variables cuantitativas y cualitativas (como por ejemplo ubicaciones, variedades de cultivos, tipos de tratamiento, …)? Pues el Análisis de Componentes Principales permite hacer todo esto de una forma tremendamente sencilla. ¡Por fin una herramienta que permite mezclar peras con manzanas!
Por si esto fuera poco, la interpretación de los resultados es también muy asequible, y la representación de las muestras y de las variables en el nuevo espacio definido por los PC permite detectar agrupaciones de muestras que deban ser analizadas por separado, relaciones directas o inversas entre variables, conocer qué medidas aportan valor para explicar lo que está sucediendo y cuáles son irrelevantes o sólo aportan ruido, detectar a simple vista muestras anómalas de entre miles… Pero todo esto lo dejaremos para otro día.
El universo del análisis multivariante incluye otras técnicas igualmente interesantes, como la regresión por mínimos cuadrados parciales (PLS, algo así como el superhéroe de las regresiones) o las técnicas combinadas de agrupación (tipo PLS-DA) que son especialmente útiles para múltiples aplicaciones como la calibración de equipos y métodos o para entender procesos o fenómenos complejos.
Apunte terminológico.
Los vectores que determinan las direcciones de máxima varianza (es decir, los vectores directores de los Componentes Principales) se llaman eigenvectors.
Los eigenvalues son una medida de la varianza explicada por cada uno de los Componentes Principales, es decir, de la magnitud de cada uno de estos nuevos ejes. A cada eigenvector le corresponde un eigenvalue.
Las coordenadas de las muestras en el espacio definido por los Componentes Principales se denominan scores.
Las coordenadas de las variables en el espacio definido por los Componentes Principales (es decir, los coeficientes que acompañan a cada variable en la definición matemática de cada PC como combinación lineal de las variables originales) se llaman loadings.
P.D.: para escribir este post he preparado el ejemplo en una hoja de Excel, haciendo un pequeño ejercicio geométrico para calcular los vectores directores y vectores unitarios de los ejes r y s, calcular el RMSE y representarlo todo gráficamente, incluyendo los errores y el cambio de coordenadas. Si alguien está interesado en el archivo como herramienta didáctica para jugar con los datos y ver gráficamente cómo cambian las direcciones de máxima varianza, escriban un email (victor@victorfalguera.cat) y lo enviaré sin problema.